The music is very structured, which allows it to be played by a rather simple mechanism. Here’s a rolling ball machine that plays the pattern.

Poetry

“Decision Tree”
The Abacaba pattern is central in the binary tree fractal. This tree could be a model of all of your paths in life. Every time you make a decision, the universe splits in two copies that are nearly alike, but depending on what your decision is, you could end up in two entirely different places! If only we could have a map of all of future decisions and where they lead, then we could see where we want to go and know exactly how to get there. 

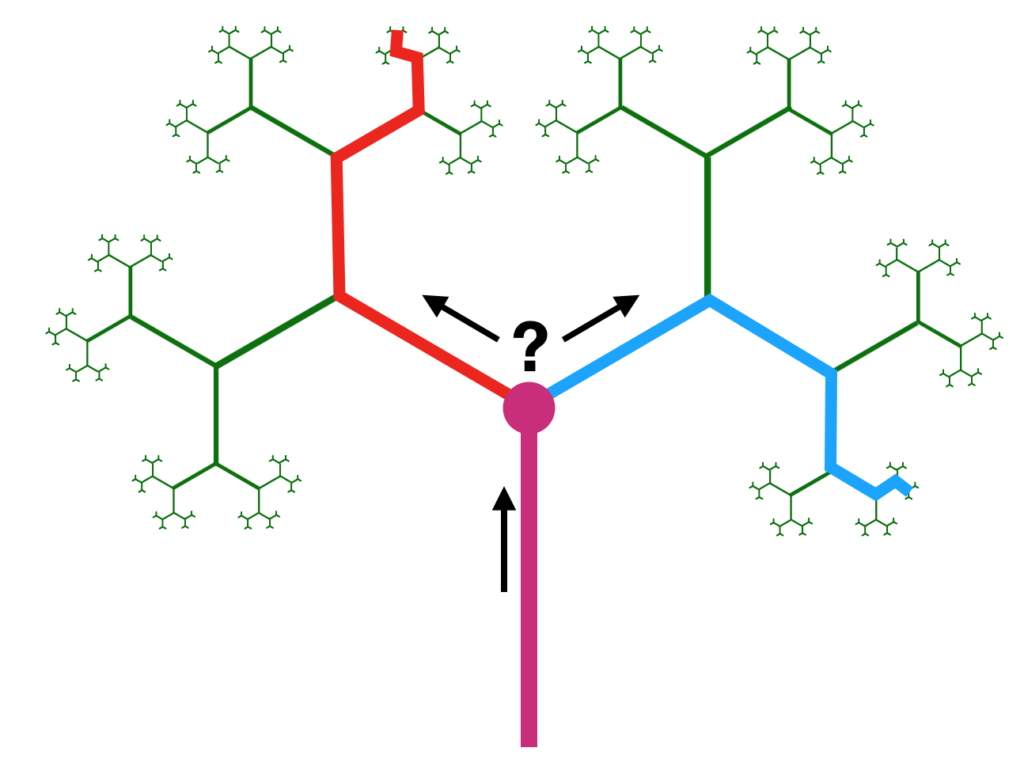
That’s the idea of this poem, Decision Tree. Start at the trunk of the tree… and choose wisely!

The poem was designed with the trunk as the question, the first branches as the decision, the next as the narrator’s reaction, and finally how the decision affects the future. In addition, movements to left are a bit devilish while those to the right are a bit angelic.
Interestingly, most of the paths create poems that are a little depressing, but there are two where you get the feeling the narrator is feels pretty good about him/her-self… the path entirely to the left and the path entirely to the right! In life, as in mathematics, we are free to make our own rules. After we’ve chosen the rules, we need to be consistent or we risk an unsatisfying result!

“Entirely Nothing”

The Cantor Set is a fractal made from a line segment. Remove the middle third. In each of the remaining parts, remove the middle thirds again. Repeat on these smaller parts and continue infinitely. The resulting shape has infinitely many points, but a combined length of zero!
At each step in making the Cantor Set, we find an Abacaba pattern. It’s in the spaces between the lines. As the original line segment shrinks to nothing, the Abacaba pattern grows infinitely!
Here’s a poem with this structure.