The homepage of one of the most fascinating patterns
“Abacaba” is a fascinating pattern that is found in all kinds of surprising places. Here you can find out all about the pattern, explore connections and discover creative projects inspired by the pattern.
About… the pattern and mathematical connections
Explore… activites, music, poetry, video
Abacabax… the fantasy novel inspired by the pattern
Continue doubling and adding the next letter of the alphabet to build the pattern as far as you want to go.
Geometric lengths If we give each letter a length, doubling the length for each in order, we get this pattern:
This is the same pattern on an English ruler:
Trees Rotate this 90° and we can see the shape of a play-off tree:
Rotate 90° again and we final a fractal binary tree. We could think of this as a family tree … everyone comes from two parents, each of them with two parents, and so on. That means every person is right in the middle of their own Abacaba pattern!
Here’s the same shape with the branches at 120° angles. You’ll find variations of this shape all over nature: in plants and in the human body for example.
Fractals Here’s another famous fractal, the Sierpinski triangle, made from removing the center of a triangle and then removing the centers of the remaining triangles, and so on. It’s full of Abacaba patterns …
Here’s a few of them. There are infinitely many more!
The Mandelbrot set is a well-known fractal built on the complex plane.
Zoom in on the nose to the left and you’ll see the Abacaba pattern rippling off to infinity!
Cantor dust is created by staring with a line segment and removing the center third. Each of the remaining pieces has the center thirds removed, and so on. Here are the first few stages… the holes make an Abacaba pattern:
When the process is carried out to its limit at infinity, Cantor dust has an infinite number of points, no line segments at all, and a total length of zero. The 2d version is called the Sierpinski Carpet. Start with a square, divide into a 3×3 grid and remove the center square. Repeat the process on the remaining 8 squares. The sum of the edge lengths of a Sierpinski Carpet is infinite and it has an area of zero … it becomes a sheet composed entirely of holes! Here is a mirror made with the first 5 iterations – there are over 4000 holes in the frame!
There is also a 3d version called a Menger sponge. It has infinite surface area and zero volume. Weird.
Number systems Binary numbers are used everywhere. If you pay attention to the number of zeros at the end of each number as you count in binary, you’ll find the Abacaba pattern.
If we instead start with binary 00000 and switch the digits one by one in the position of the Abacaba pattern (digit 1, then 2, then 1, then 3, and so on) we get a number sequence called the Gray code. It contains all of the integers with none repeated.
This number sequence is used in devices that sense rotation. Because only one bit is changed at a time, errors are very small. You can see that Gray code also makes a fractal binary tree!
Here’s what happens when we connect the integer sequence with a curve that passes through the numbers in the Gray code sequence. 
Hyperspace Planning to travel in hyperspace and worried about getting lost? Following the Abacaba pattern will take you to all of the corners of hypercube. Here’s four related figures in four different dimensions. Label the direction of each dimension with a different number (or letter). Start at any corner, and move according to the Abacaba pattern. You’ll visit every corner. It works in any dimension!
Watch the TEDx talk on Abacaba:
Paper folding
Music
In the fully-orchestrated version, Abacaba patterns are embedded not only as notes, but also in the rhythms and stereo.
Download sheet music for version 1 so you can play it yourself on piano.
The music is very structured, which allows it to be played by a rather simple mechanism. Here’s a rolling ball machine that plays the pattern.
Poetry
“Decision Tree”
The Abacaba pattern is central in the binary tree fractal. This tree could be a model of all of your paths in life. Every time you make a decision, the universe splits in two copies that are nearly alike, but depending on what your decision is, you could end up in two entirely different places! If only we could have a map of all of future decisions and where they lead, then we could see where we want to go and know exactly how to get there.
That’s the idea of this poem, Decision Tree. Start at the trunk of the tree… and choose wisely!
The poem was designed with the trunk as the question, the first branches as the decision, the next as the narrator’s reaction, and finally how the decision affects the future. In addition, movements to left are a bit devilish while those to the right are a bit angelic.
Interestingly, most of the paths create poems that are a little depressing, but there are two where you get the feeling the narrator is feels pretty good about him/her-self… the path entirely to the left and the path entirely to the right! In life, as in mathematics, we are free to make our own rules. After we’ve chosen the rules, we need to be consistent or we risk an unsatisfying result!
“Entirely Nothing”
The Cantor Set is a fractal made from a line segment. Remove the middle third. In each of the remaining parts, remove the middle thirds again. Repeat on these smaller parts and continue infinitely. The resulting shape has infinitely many points, but a combined length of zero!
At each step in making the Cantor Set, we find an Abacaba pattern. It’s in the spaces between the lines. As the original line segment shrinks to nothing, the Abacaba pattern grows infinitely!
Here’s a poem with this structure.
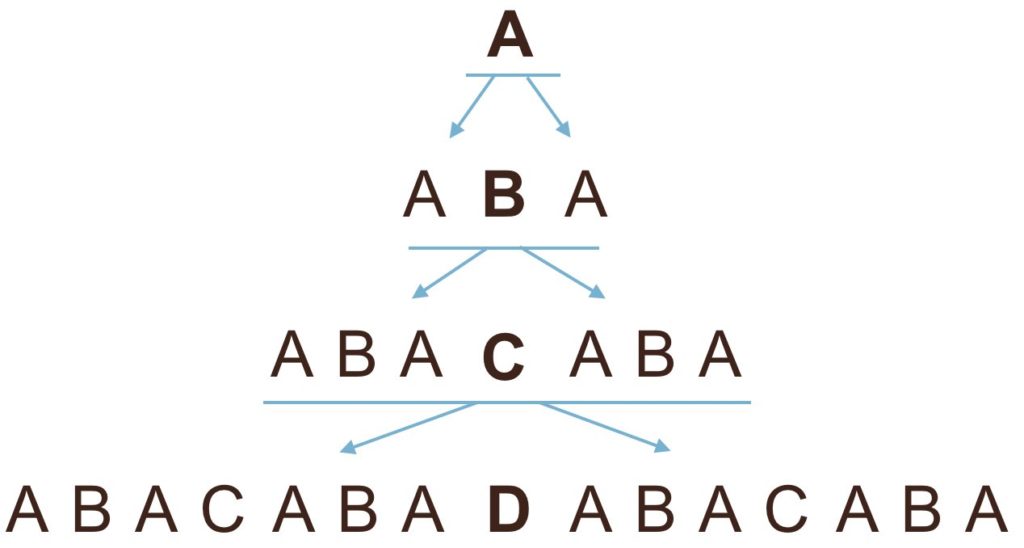
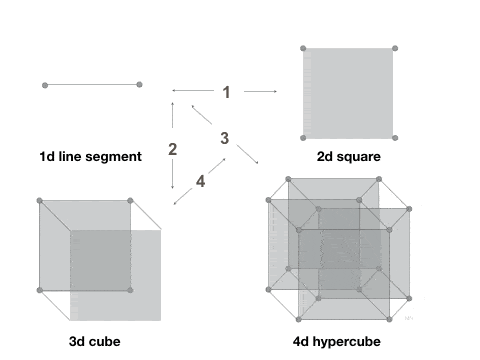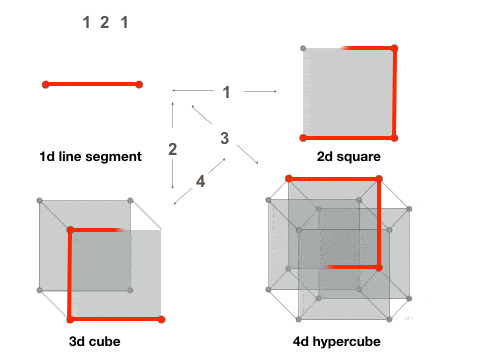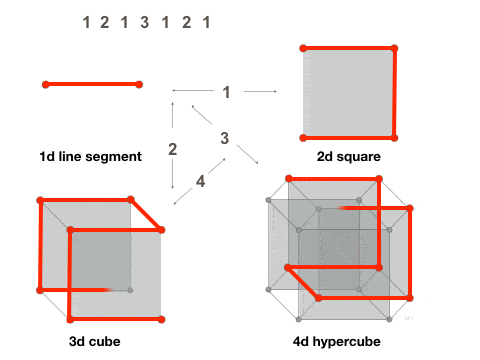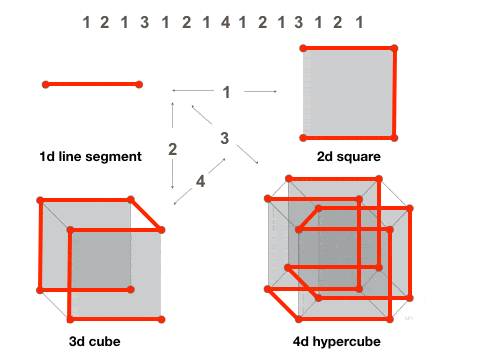
Abacabax is the new fantasy novel inspired by the Abacaba-pattern. The world is built on a 3d Abacaba-fractal, and the story is filled with structures and themes that arise from the pattern.
Synopsis
Max Teller is on the run for his life on Abacabax, a world of incredible patterns, danger and beauty that stands on the brink of destruction. Four families, each with unique abilities, are locked in a struggle for power and revenge while dark creatures have united with deadly purpose. Max is lost and alone, not knowing whom to trust and unable to awaken the powers that everyone assumes he has. Armed only with a broken abacus and his unconventional imagination, he must make unlikely allies and battle the growing awareness that he may be the one destined to destroy the world.
What they’re saying
“A fascinating story, well written and interesting. I wish it was twice as long. Recommended to anyone with an imagination and mandatory to those with an imagination and an affinity for numbers, systems and maths in general.” – goodreads
“This was a very interesting, exciting and capturing book to read. Something totally different from books in this genre that I have read before. From start to end you are taken in to a world of beauty, magic and mathematics. It is filled with strange, strong characters with different abilities, using their powers for the good and the bad. It is playful, scary, fun and with a lot of surprises. A stunning, breathtaking adventure. A real page-turner – I couldn’t put it down!” – goodreads
“I truly enjoyed reading this book. It is not only exciting… it inspired me to learn more about mathematics. The reader does not need to know much about math or even like it in order to become captivated by the story – and bewitched by the power of math or the power of recognizing patterns behind the surface … in everything from nature, the landscape, and the tools used by its inhabitants, to the hieroglyphics and the music. Abacabax seduces the reader to see the beauty and similarity behind different forms … Having read Abacabax, I bought myself an abacus for playing with numbers in a new way.” – amazon.co.uk
Available now
Paperback, 370 pages. Includes chapter illustrations, maps and addenda detailing the reckoning methods of the four families. Learn to reckon like a Dijin, Bone-Thrower, Calculist and Abacist!
Available now on Amazon in both paperbook and eBook format.
This site is created and maintained by Mike Naylor. Have a question or a request? Send me a message!